TreeGrid
Treegrid is a way to represent hierarchical data in grid.
Treegrid supports both the Nested Set model and the Adjacency model. Good articles describing the Nested Set model can be found here:
http://dev.mysql.com/tech-resources/articles/hierarchical-data.html
http://www.sitepoint.com/article/hierarchical-data-database
Installation
In order to use this module you should mark the Treegrid when you download the grid. For more information refer to Download.
For Developers - this is the grid.treegrid.js in the src directory.
Options
The following options can be set in the grid options to configure the treeGrid
| Option | Type | Description | Default |
|---|---|---|---|
| ExpandColClick | boolean | when true, the tree is expanded and/or collapsed when we click on the text of the expanded column, not only on the image | true |
| ExpandColumn | string | indicates which column (name from colModel) should be used to expand the tree grid. If not set the first one is used. Valid only when treeGrid option is set to true. | null |
| treedatatype | mixed | Determines the initial datatype (see datatype option). Usually this should not be changed. During the reading process this option is equal to the datatype option. | null |
| treeGrid | boolean | Enables (disables) the tree grid format. | false |
| treeGridModel | string | Deteremines the method used for the treeGrid. Can be nested or adjacency. | nested |
| treeIcons | array | This array set the icons used in the tree. The icons should be a valid names from UI theme roller images. The default values are: {plus:'ui-icon-triangle-1-e',minus:'ui-icon-triangle-1-s',leaf:'ui-icon-radio-off'} | |
| treeReader | array | extends the colModel defined in the basic grid. The fields described here are added to end of the colModel array and are hidden. This means that the data returned from the server should have values for these fields. For a full description of all valid values see below. | |
| tree_root_level | numeric | Determines the level where the root element begins when treeGrid is enabled | 0 |
The treeReader property adds dynamically columns to the colModel property of the basic grid when treeGrid property is set to true. Syntax:
treeReader : { property1 : value1 ... propertyN : valueN }
The treeReader property is adds diffrent columns in the colModel depending on the treeGridModel property - i.e. we have diffrent configurations for different models - Nested Set Model and Adjacency Model.
Currently jqGrid can work only with data returned from server. There are some tricks and articles wich describes how to work with local data.
SELECT category_name, level, lft, rgt FROM categories ORDER BY lft;
Methods
In the methods below, record means the current record, which can be obtained via the getInd method like this:
var record = jQuery("#grid_id").getInd(rowid,true);
NOTE: This no longer works as of version 3.7.x. Use var record = jQuery(”#grid_id”).getRowData(rowid); instead.
Where rowid is the id of the row. Note the second parameter in the method. If the second parameter is omited or set to false (default) the returned value is the index of the row. If the row can not be found a false is returned.
| Method | Parameters | Description |
|---|---|---|
| collapseNode | record | Collapse the node at specified record |
| collapseRow | record | Collapse the current row |
| delTreeNode | rowid | Where rowid is the id of the row. Deletes the specified node and all child nodes of that node. Does not delete the node at server |
| expandNode | record | Expand the node at the specified record |
| expandRow | record | Expand the current row |
| getNodeAncestors | record | returns array of the ancestors of the specified record |
| getNodeDepth | record | returns the depth of the specified record |
| getNodeParent | record | Returns the parent node of the specified record |
| getNodeChildren | record | Returns array of child nodes of the specified record; returns empty array if none |
| getRootNodes | none | Returns an array of the current root nodes. |
| isNodeLoaded | record | Returns true if the node is already loaded |
| isVisibleNode | record | Returns true or false if the node is visible or not |
| setTreeRow | rowid, data | The same as setRowData |
| SortTree | direction | Direction is 1 (meaning ascending) or -1 (meaning descending); sorts the tree with the currently set sortname (sortname is from grid option) |
Cautions and Limitations
- Currently adding nodes with addRowData is not supported.
Currently it is not recommended to combine inline editing and form editing with treegrid, or the expanded column will not be editable.- Adding nodes is currently not supported.
- Pager functionality currently disabled for treeGrid
- When we initialize the grid and the data is read, the datatype is automatically set to local. This is required because treegrid supports autoloading tree nodes. This means that, for speed or efficiency, you can load the data only for the root level first and load the data for a particular child node only when the operator clicks to expand that node. The grid will determine that there is no data and try to load the node from the server, but in this case the data that is sent to the server has to have additional parameters. Setting datatype to local permits intervening before the request is made to build the request correctly. See the Nested Set Model and Adjacency Model on what is posted to the server
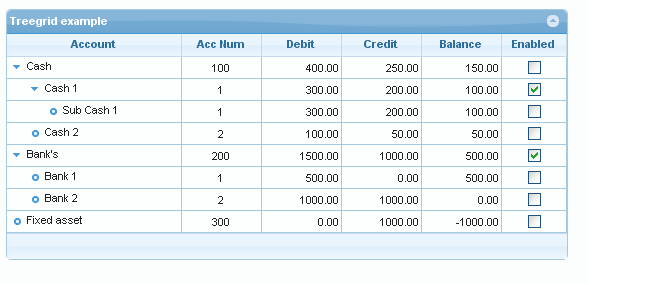
Discussion
The need for
treedatatype?Short Story: Should we remove
treedatatypefrom the code? It appears to be a synonym fordatatype.Background: I recently had a bug in my code where I set
treedatatype:'json', but forgot to setdatatype(admitted jqGrid newbie mistake). The result was a treeGrid that failed to load initially, but successfully loaded after refresh. Digging into grid.base.js and grid.treegrid.js, I noticed thattreedatatypeis originally set todatatype, thendatatypeis later overwritten withtreedatatype.Should we remove
treedatatype? …or is there another (or future) use fortreedatatypethat I am missing?Thank you
Is there any events support for treegrid just like 'onNodeExpanded' or 'onNodeCollapsed' ?
Thank you.
Hello, Currently no. The treeGrid component will be developed in the future with the ability not only for this, but to insert, add and delete tree nodes.
Tony