This is an old revision of the document!
Table of Contents
Common rules
Grouping is a way to group data by diffrent criteria. jqGrid support currently one level grouping.
The simple way to group in jqGrid is to enable grouping with the grid option grouping:true and define a field name on which grouping occur. The name should correspondent of the name in colModel The definituion is done with array groupField which is a part of another grid option groupingView.
It is important to note that if you want grouping to be correct, then the data should come from server to grid sorted by that field. When we are in local mode (the data is array) the data is grouped (sorted) automatically so there is no need to define additional sort column.
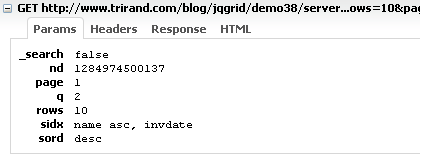
In order to inform the server that we want to have a grouped data, jqGrid add to the sidx parameter the groupField name on which we group. This done only if we have enabled the grouping and the data is remote.
For example if the grouping configuration is defined as:
jQuery("#grid").jqGrid({ ... grouping:true, groupingView : { groupField : ['name'], groupDataSorted : true }, caption: "Grouping" });
then the request send to the server will look like this (using FireBug)
We should get this information from the request, perform the appropriate sorting server side and return the requested data to the grid. The grid then get the data and do the grouping adding the appropriate (defined) headers and footers.
Limitations
- Currently only one level grouping is supported.
- When the grouping is enabled, the following options will be set explicit into the code:
- scroll = false;
- rownumbers = false;
- subGrid = false;
- treeGrid = false;
- gridview = true;
Please refer in grid options for detailed information on what these options mean
Options and methods
Options
All options in grouping are set as grid options and can be changed dynamically using the setGridParam method. Two options are related to grouping
- grouping
- groupingView
The first option grouping is Boolean and enables or disables the grouping feature into the grid. The default values of this option is false. To enable grouping set it to true - i.e grouping : true
The groupingView option is actually a object and consist a lot of other options. Below is a example on how this should be used:
jQuery("#grid").jqGrid({ ... groupingView : { groupField : ['name'], groupDataSorted : true } ... });
Below is the list of the options that are part of groupingView option
| Property | Type | Description | Default |
|---|---|---|---|
| groupField | array | Defines the name from colModel on which we group. The first value is the first lavel, the second values is the second level and etc. Currently only one level is supported | empty |
| groupOrder | array | 1 | empty |
| groupText | array | 1 | empty |
| groupColumnShow | array | 1 | empty |
| groupSummary | array | 1 | empty |
| showSummaryOnHide | boolean | 1 | false |
| groupDataSorted | boolean | 1 | false |
| groupCollapse | boolean | 1 | false |
| plusicon | string | 1 | ui-icon-circlesmall-plus |
| minusicon | string | 1 | ui-icon-circlesmall-minus |
Discussion
How do you set the text of the summary row?
i.e. if summaryTpl lets you format the sum for instance, how do you get the word 'Sum' or 'Total' to show in another column?
To create a row with just text, you'll need to use a custom summaryType function that returns a blank string.
{… summaryTpl: '<div style=“text-align: right”><b>Total Amount: </b></div>', summaryType: blankSummaryType}function blankSummaryType() { return ””; }… is much easier. :)
“groupText” propert should be allowed to be a callback function. Otherwise it's really pain in the ass to manage to fill those lines with data.
Is it possible to sort by the summarized data? IE, once the grid is grouped, I need to sort by the grouped summary data.
When using
groupDataSorted=truethe sort parameter (sidx) that is set does not reflect index values set on the column model.That is to say, if I have a column defined as:
{name: 'name', index: 'indexIsDifferentFromName'}and I am grouping by field
'name', when the sort parameter (sidx) is set on the server request it is set as'name' and not'indexIsDifferentFromName'Hi All, is it possible to use different formatter for the data rows and the summary row? If I want to add a summary info (summaryType= count) to a checkbox formatted column, summary value is shown as a checked checkbox. any ideas?
kinds, Alper
Hi!!
I'm having a pretty issue, that seems to be related with ordering… The grouping repeats when a change on the data set is received, so if I have a grouping on field 'Name', and data set values are :
Name
–
John
John
Peter
Peter
John
John
John
Paul
Paul
John
Then, the grouping will throw this:
± John - 2 regs
± Peter- 2 regs
± John - 3 regs
± Paul - 2 regs
± John - 1 regs
This is my Grid code (regarding grouping)…
groupingView: { groupField: ['Name'], groupColumnShow: [false], groupText: ['<b>{0} - {1} reg(s)</b>'], groupCollapse: true, groupDataSorted: true, groupOrder: ['asc'] }CAN ANYBODY HELP? Thanks!
Hi all,
Has anyone been able to modify the Summary/Grouping behavior to allow you to add summary statistics to the Header of each group? For example, I have grouping enabled for a number of projects - the only field I want summarized is 'funding' … so rather than waste an entire row to display a sum('funding'), I'd like to be able to include it in the groupText element. Something along these lines:
groupText : ['<b>{0} - {1} Entries, Total Dollars: {sum(funding)} </b>']
Thanks! jp